George Boole believed in what he called the ‘process of analysis’, that is, the process by which combinations of interpretable symbols are obtained. It is the use of these symbols according to well-determined methods of combination that he believed presented ‘true calculus’.

Today, all our computers use Boole's logic system - using microchips that contain thousands of tiny electronic switches arranged into logical ‘gates’ that produce predictable and reliable conclusions.

The basic logic gates are AND, OR and NOT. It is these gates, used in different combinations, that allow the computer to execute its operations using binary language.

Each gate assesses information (consisting of high or low voltages) in accordance with predetermined rules, and produces a single high or low voltage logical conclusion. The voltage itself represents the binary yes-no, true-false, one-zero concept.

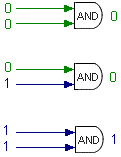AND gates will only yield a TRUE result (that is, a binary 1) if all input is TRUE. Therefore, the top two gates will produce a FALSE (binary 0) result.

OR gates are less fussy. An OR gate will send a TRUE result if any of its input is TRUE. Only if every input is FALSE will it produce a 0 result.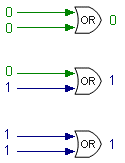

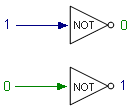NOT gates, on the other hand, do just one thing. A NOT gate accepts only a single input, either TRUE or FALSE, which it promptly reverses. NOT gates can be combined with AND or OR to give NAND (not and) or NOR (not or) gates. These new gates process input in the usual manner and then reverse the result.

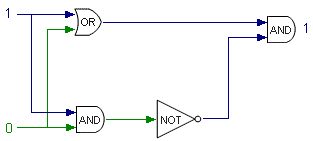
Putting them all together produces something like this (‘this’, by the way, is known as a half-adder). The top gate inputs 1 and 0 through OR to give a 1 result. The bottom gate channels 1 and 0 through AND to produce 0, which is inverted through the NOT gate into a second 1. The last AND gate sees two inputs of 1 and promptly spits out a TRUE (1) result. Thus, 1 + 0 = 1.

. . . . . . . . . . . . . . . . . . . .

By adjusting the gates, binary adders can be used not only for addition, but for subtraction, multiplication, and division as well, enabling them to control the computer's data flow and to process instructions.

Related:
George Boole
Binary - So Simple a Computer Can Do It